Building a Named Entity Recognition model using a BiLSTM-CRF network
Nikolay Manchev2021-07-01 | 14 min read
In this blog post we present the Named Entity Recognition problem and show how a BiLSTM-CRF model can be fitted using a freely available annotated corpus and Keras. The model achieves relatively high accuracy and all data and code is freely available in the article.
What is Named Entity Recognition?
Named Entity Recognition (NER) is an NLP problem, which involves locating and classifying named entities (people, places, organizations etc.) mentioned in unstructured text. This problem is used in many NLP applications that deal with use-cases like machine translation, information retrieval, chatbots and others.
The categories that the named entities are classified into are predefined and often contain entries like locations, organisations, job types, personal names, times and others.
An example of unstructured text presented to an NER system could be:
"President Joe Biden visits Europe in first presidential overseas trip"
After processing the input, a NER model could output something like this:
[President]Title [Biden]Name visits [Europe]Geography in first presidential overseas trip
It follows from this example, that the NER task can be broken down into two independent tasks:
- first, we need to establish the boundaries of each entity (i.e. we need to tokenize the input)
- second, we need to assign each entity to one of the predefined classes
Approaching a Named Entity Recognition (NER) problem
An NER problem can be generally approached in two different ways:
- grammar-based techniques - This approach involves experienced linguists who manually define specific rules for entity recognition (e.g. if an entity name contains the token "John" it is a person, but if it also contains the token "University" then it is an organisation). This type of hand-crafted rule yields very high precision, but it requires a tremendous amount of work to define entity structures and capture edge cases. Another drawback is that keeping such a grammar-based system up to date requires constant manual intervention and is a laborious task.
- statistical model-based techniques - Using Machine Learning we can streamline and simplify the process of building NER models, because this approach does not need a predefined exhaustive set of naming rules. The process of statistical learning can automatically extract said rules from a training dataset. Moreover, keeping the NER model up to date can also be performed in an automated fashion. The drawback with statistical model-based techniques is that the automated extraction of a comprehensive set of rules requires a large amount of labeled training data.
How to build a statistical Named Entity Recognition (NER) model
In this blog post we will focus on building a statistical NER model, using the freely available Annotated Corpus for Named Entity Recognition. This dataset is based on the GMB (Groningen Meaning Bank) corpus, and has been tagged, annotated and built specifically to train a classifier to predict named entities such as name, location, etc. The tags used in the dataset follow the IOB format, which we cover in the next section.
The IOB format
Inside–outside–beginning (IOB) is a common format for tagging entities in computer linguistics, especially in a NER context. This scheme was initially proposed by Ramshaw and Marcus (1995), and the meaning of the IOB tags is as follows:
- the I-prefix indicates that the tag is inside a chunk (i.e. a noun group, a verb group etc.)
- the O-prefix indicates that the token belongs to no chunk
- the B-prefix indicates that the tag is at the beginning of a chunk that follows another chunk without O tags between the two chunks
The entity tags used in the sample dataset are as follows:
Tag | Meaning | Example |
|---|---|---|
geo | Geography | Britain |
org | Organisation | IAEA |
per | Person | Thomas |
gpe | Geopolitical Entity | Pakistani |
tim | Time | Wednesday |
art | Artifact | Pentastar |
eve | Event | Armistice |
nat | Natural Phenomenon | H5N1 |
The following example shows the application of IOB on the class labels:
Token | Tag | Meaning |
|---|---|---|
George | B-PER | Beginning of a chunk (B tag), classified as Person |
is | O | token belongs to no chunk |
travelling | O | token belongs to no chunk |
to | O | token belongs to no chunk |
England | I-GEO | Inside of a chunk (I tag), classified as Geography |
on | O | token belongs to no chunk |
Sunday | I-TIM | Inside of a chunk, classified as Time |
The CRF model
Conditional random field (CRF) is a statistical model well suited for handling NER problems, because it takes context into account. In other words, when a CRF model makes a prediction, it factors in the impact of neighbouring samples by modelling the prediction as a graphical model. For example, a linear chain CRF is a popular type of a CRF model, which assumes that the tag for the present word is dependent only on the tag of just one previous word (this is somewhat similar to Hidden Markov Models, although CRF's topology is an undirected graph).
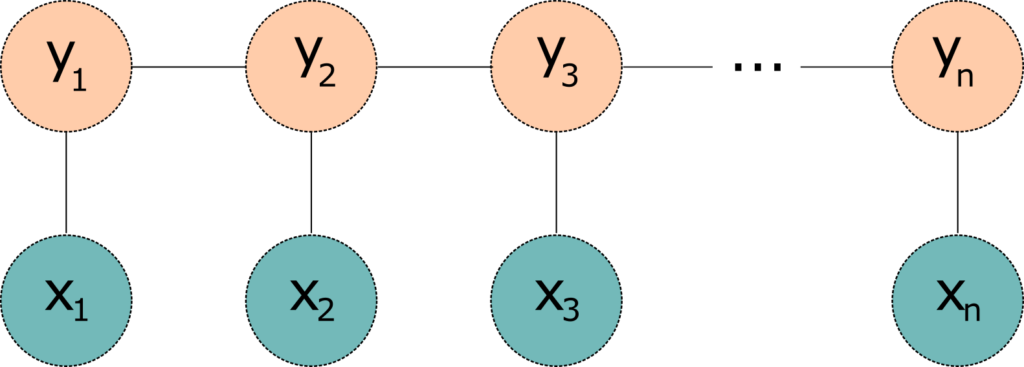
Figure 1 : A simple linear-chain conditional random fields model. The model takes an input sequence x (words) and target sequence y (IOB tags)
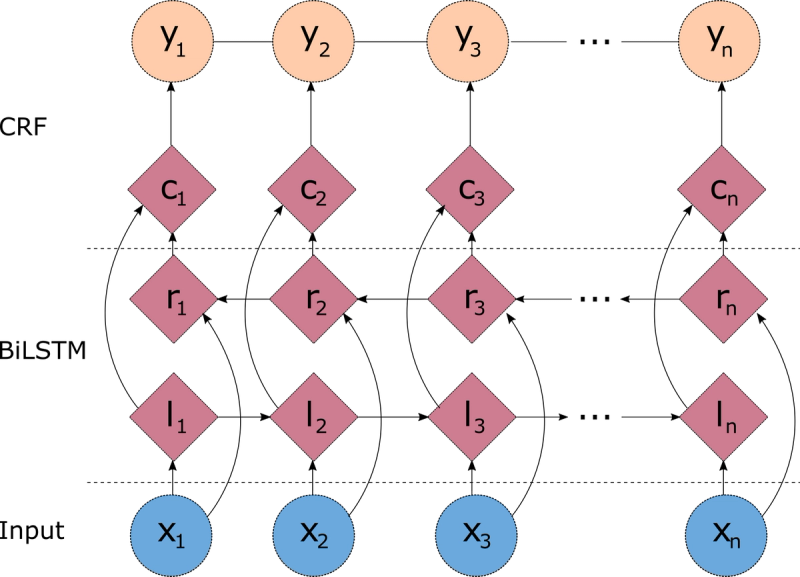
One problem with the linear chain CRFs (Figure 1) is that they are capable of capturing the dependencies between labels in the forward direction only. If the model encounters an entity like "Johns Hopkins University" it will likely tag the Hopkins token as a name, because the model is "blind" to the university token that appears downstream. One way to resolve this challenge is to introduce a bidirectional LSTM (BiLSTM) network between the inputs (words) and the CRF. The bidirectional LSTM consists of two LSTM networks - one takes the input in a forward direction, and a second one taking the input in a backward direction. Combining the outputs of the two networks yields a context that provides information on samples surrounding each individual token. The output of the BiLSTM is then fed to a linear chain CRF, which can generate predictions using this improved context. This combination of CRF and BiLSTM is often referred to as a BiLSTM-CRF model (Lample et al 2016), and its architecture is shown in Figure 2.
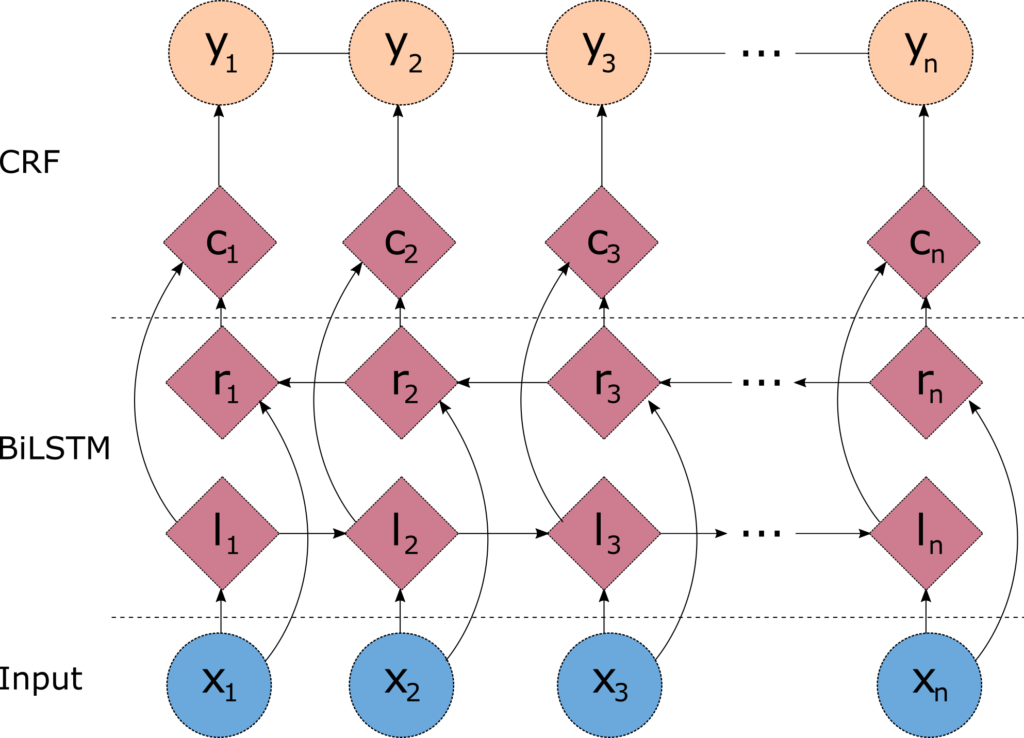
Figure 2 - Architecture of a BiLSTM-CRF model
Data exploration and preparation
We start by importing all the libraries needed for the ingestion, exploratory data analysis, and model building.
import pickle
import operator
import re
import string
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from plot_keras_history import plot_history
from sklearn.model_selection import train_test_split
from sklearn.metrics import multilabel_confusion_matrix
from keras_contrib.utils import save_load_utils
from keras import layers
from keras import optimizers
from keras.models import Model
from keras.models import Input
from keras_contrib.layers import CRF
from keras_contrib import losses
from keras_contrib import metricsNext, we read and take a peek at the annotated dataset.
data_df = pd.read_csv("dataset/ner_dataset.csv", encoding="iso-8859-1", header=0)
data_df.head()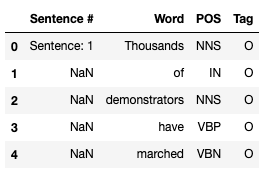
The meaning of the attributes is as follows:
- Sentence # - sentence ID
- Word - contains all words that form individual sentences
- POS - Part of Speech tag for each word, as defined in the Penn Treebank tagset
- Tag - IOB tag for each word
Looking at the data, we see that the sentence ID is given only once per sentence (with the first word of the chunk), and the remaining values for "Sentence #" attribute are set to NaN. We will remedy this by repeating the ID for all remaining words, so that we can calculate meaningful statistics.
data_df = data_df.fillna(method="ffill")
data_df["Sentence #"] = data_df["Sentence #"].apply(lambda s: s[9:])
data_df["Sentence #"] = data_df["Sentence #"].astype("int32")
data_df.head()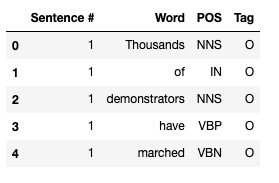
Now let's calculate some statistics about the data.
print("Total number of sentences in the dataset: {:,}".format(data_df["Sentence #"].nunique()))
print("Total words in the dataset: {:,}".format(data_df.shape[0]))Total number of sentences in the dataset: 47,959
Total words in the dataset: 1,048,575data_df["POS"].value_counts().plot(kind="bar", figsize=(10,5));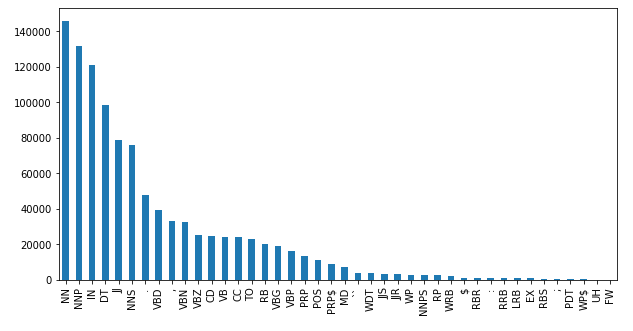
We notice that the top 5 parts of speech in the corpus are:
- NN - noun (e.g. table)
- NNP - proper noun (e.g. John)
- IN - preposition (e.g. in, of, like)
- DT - determiner (the)
- JJ - adjective (e.g. green)
data_df[data_df["Tag"]!="O"]["Tag"].value_counts().plot(kind="bar", figsize=(10,5))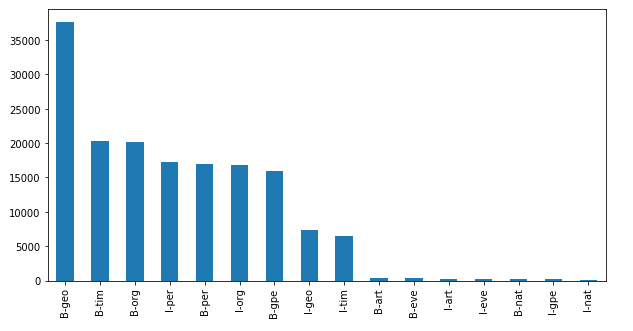
Based on the plot above we learn that many of our sentences start with a geography, time, organisation, or a person.
We can now look at the distribution of words per sentence.
word_counts = data_df.groupby("Sentence #")["Word"].agg(["count"])
word_counts = word_counts.rename(columns={"count": "Word count"})
word_counts.hist(bins=50, figsize=(8,6));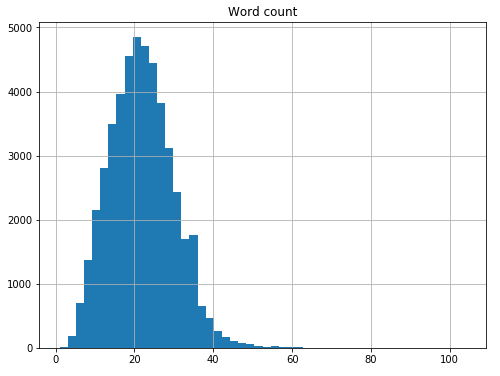
We see that the average sentence in the dataset contains about 21-22 words.
MAX_SENTENCE = word_counts.max()[0]
print("Longest sentence in the corpus contains {} words.".format(MAX_SENTENCE))Longest sentence in the corpus contains 104 words.longest_sentence_id = word_counts[word_counts["Word count"]==MAX_SENTENCE].index[0]
print("ID of the longest sentence is {}.".format(longest_sentence_id))ID of the longest sentence is 22480.longest_sentence = data_df[data_df["Sentence #"]==longest_sentence_id]["Word"].str.cat(sep=' ')
print("The longest sentence in the corpus is:\n")
print(longest_sentence)The longest sentence in the corpus is: Fisheries in 2006 - 7 landed 1,26,976 metric tons , of which 82 % ( 1,04,586 tons ) was krill ( Euphausia superba ) and 9.5 % ( 12,027 tons ) Patagonian toothfish ( Dissostichus eleginoides - also known as Chilean sea bass ) , compared to 1,27,910 tons in 2005 - 6 of which 83 % ( 1,06,591 tons ) was krill and 9.7 % ( 12,396 tons ) Patagonian toothfish ( estimated fishing from the area covered by the Convention of the Conservation of Antarctic Marine Living Resources ( CCAMLR ) , which extends slightly beyond the Southern Ocean area ).all_words = list(set(data_df["Word"].values))all_tags = list(set(data_df["Tag"].values))
print("Number of unique words: {}".format(data_df["Word"].nunique()))
print("Number of unique tags : {}".format(data_df["Tag"].nunique()))Number of unique words: 35178
Number of unique tags : 17Now that we are slightly more familiar with the data, we can proceed with implementing the necessary feature engineering. The first step is to build a dictionary (word2index) that assigns a unique integer value to every word from the corpus. We also construct a reversed dictionary that maps indices to words (index2word).
word2index = {word: idx + 2 for idx, word in enumerate(all_words)}
word2index["--UNKNOWN_WORD--"]=0
word2index["--PADDING--"]=1
index2word = {idx: word for word, idx in word2index.items()}Let's look at the first 10 entries in the dictionary. Note that we have included 2 extra entries at the start - one for unknown words and one for padding.
for k,v in sorted(word2index.items(), key=operator.itemgetter(1))[:10]:
print(k,v)--UNKNOWN_WORD-- 0
--PADDING-- 1
truck 2
87.61 3
HAMSAT 4
gene 5
Notre 6
Samaraweera 7
Frattini 8
nine-member 9Let's confirm that the word-to-index and index-to-word mapping works as expected.
test_word = "Scotland"
test_word_idx = word2index[test_word]
test_word_lookup = index2word[test_word_idx]
print("The index of the word {} is {}.".format(test_word, test_word_idx))
print("The word with index {} is {}.".format(test_word_idx, test_word_lookup))The index of the word Scotland is 15147.
The word with index 15147 is Scotland.Let's now build a similar dictionary for the various tags.
tag2index = {tag: idx + 1 for idx, tag in enumerate(all_tags)}
tag2index["--PADDING--"] = 0
index2tag = {idx: word for word, idx in tag2index.items()}Next, we write a custom function that will iterate over each sentence, and form a tuple consisting of each token, the part of speech the token represents, and its tag. We apply this function to the entire dataset and then see what the transformed version of the first sentence in the corpus looks like.
def to_tuples(data):
iterator = zip(data["Word"].values.tolist(),
data["POS"].values.tolist(),
data["Tag"].values.tolist())
return [(word, pos, tag) for word, pos, tag in iterator]
sentences = data_df.groupby("Sentence #").apply(to_tuples).tolist()
print(sentences[0])[('Thousands', 'NNS', 'O'),
('of', 'IN', 'O'),
('demonstrators', 'NNS', 'O'),
('have', 'VBP', 'O'),
('marched', 'VBN', 'O'),
('through', 'IN', 'O'),
('London', 'NNP', 'B-geo'),
('to', 'TO', 'O'),
('protest', 'VB', 'O'),
('the', 'DT', 'O'),
('war', 'NN', 'O'),
('in', 'IN', 'O'),
('Iraq', 'NNP', 'B-geo'),
('and', 'CC', 'O'),
('demand', 'VB', 'O'),
('the', 'DT', 'O'),
('withdrawal', 'NN', 'O'),
('of', 'IN', 'O'),
('British', 'JJ', 'B-gpe'),
('troops', 'NNS', 'O'),
('from', 'IN', 'O'),
('that', 'DT', 'O'),
('country', 'NN', 'O'),
('.', '.', 'O')]We use this transformed dataset to extract the features (X) and labels (y) for the model. We can see what the first entries in X and y look like, after the two have been populated with words and tags. We can discard the part of speech data, as it is not needed for this specific implementation.
X = [[word[0] for word in sentence] for sentence in sentences]
y = [[word[2] for word in sentence] for sentence in sentences]
print("X[0]:", X[0])
print("y[0]:", y[0])X[0]: ['Thousands', 'of', 'demonstrators', 'have', 'marched', 'through', 'London', 'to', 'protest', 'the', 'war', 'in', 'Iraq', 'and', 'demand', 'the', 'withdrawal', 'of', 'British', 'troops', 'from', 'that', 'country', '.']
y[0]: ['O', 'O', 'O', 'O', 'O', 'O', 'B-geo', 'O', 'O', 'O', 'O', 'O', 'B-geo', 'O', 'O', 'O', 'O', 'O', 'B-gpe', 'O', 'O', 'O', 'O', 'O']We also need to replace each word with its corresponding index from the dictionary.
X = [[word2index[word] for word in sentence] for sentence in X]
y = [[tag2index[tag] for tag in sentence] for sentence in y]
print("X[0]:", X[0])
print("y[0]:", y[0])X[0]: [19995, 10613, 3166, 12456, 20212, 9200, 27, 24381, 28637, 2438, 4123, 7420, 34783, 18714, 14183, 2438, 26166, 10613, 29344, 1617, 10068, 12996, 26619, 14571]
y[0]: [17, 17, 17, 17, 17, 17, 4, 17, 17, 17, 17, 17, 4, 17, 17, 17, 17, 17, 13, 17, 17, 17, 17, 17]We see that the dataset has now been indexed. We also need to pad each sentence to the maximal sentence length in the corpus, as the LSTM model expects a fixed length input. This is where the extra "--PADDING--" key in the dictionary comes into play.
X = [sentence + [word2index["--PADDING--"]] * (MAX_SENTENCE - len(sentence)) for sentence in X]
y = [sentence + [tag2index["--PADDING--"]] * (MAX_SENTENCE - len(sentence)) for sentence in y]
print("X[0]:", X[0])
print("y[0]:", y[0])X[0]: [19995, 10613, 3166, 12456, 20212, 9200, 27, 24381, 28637, 2438, 4123, 7420, 34783, 18714, 14183, 2438, 26166, 10613, 29344, 1617, 10068, 12996, 26619, 14571, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
y[0]: [17, 17, 17, 17, 17, 17, 4, 17, 17, 17, 17, 17, 4, 17, 17, 17, 17, 17, 13, 17, 17, 17, 17, 17, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]The last transformation we need to perform is to one-hot encode the labels.:
TAG_COUNT = len(tag2index)
y = [ np.eye(TAG_COUNT)[sentence] for sentence in y]
print("X[0]:", X[0])print("y[0]:", y[0])X[0]: [19995, 10613, 3166, 12456, 20212, 9200, 27, 24381, 28637, 2438, 4123, 7420, 34783, 18714, 14183, 2438, 26166, 10613, 29344, 1617, 10068, 12996, 26619, 14571, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
y[0]: [[0. 0. 0. ... 0. 0. 1.]
[0. 0. 0. ... 0. 0. 1.]
[0. 0. 0. ... 0. 0. 1.]
...
[1. 0. 0. ... 0. 0. 0.]
[1. 0. 0. ... 0. 0. 0.]
[1. 0. 0. ... 0. 0. 0.]]Finally, we split the resulting dataset into a training and hold-out set, so that we can measure the performance of the classifier on unseen data.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=1234)
print("Number of sentences in the training dataset: {}".format(len(X_train)))
print("Number of sentences in the test dataset : {}".format(len(X_test)))Number of sentences in the training dataset: 43163
Number of sentences in the test dataset : 4796We can also convert everything into NumPy arrays, as this makes feeding the data to the model simpler.
X_train = np.array(X_train)
X_test = np.array(X_test)
y_train = np.array(y_train)
y_test = np.array(y_test)Modelling
We start by calculating the maximal word length. We also set the following model hyperparameters:
- DENSE_EMBEDDING - Dimension of the dense embedding
- LSTM_UNITS - Dimensionality of the LSTM output space
- LSTM_DROPOUT - Fraction of the LSTM units to drop for the linear transformation of the recurrent state
- DENSE_UNITS - Number of fully connected units for each temporal slice
- BATCH_SIZE - Number of samples in a training batch
- MAX_EPOCHS - Maximum number of training epochs
WORD_COUNT = len(index2word)DENSE_EMBEDDING = 50LSTM_UNITS = 50LSTM_DROPOUT = 0.1DENSE_UNITS = 100BATCH_SIZE = 256MAX_EPOCHS = 5We proceed by defining the architecture of the model. We add an input layer, an embedding layer (to transform the indexes into dense vectors, a bidirectional LSTM layer, and a time-distributed layer (to apply the dense output layer to each temporal slice). We then pipe this to a CRF layer, and finally construct the model by defining its input as the input layer and its output as the output of the CRF layer.
We also set a loss function (for linear chain Conditional Random Fields this is simply the negative log-likelihood) and specify "accuracy" as the metric that we'll be monitoring. The optimiser is set to Adam (Kingma and Ba, 2015) with a learning rate of 0.001.
input_layer = layers.Input(shape=(MAX_SENTENCE,))
model = layers.Embedding(WORD_COUNT, DENSE_EMBEDDING, embeddings_initializer="uniform", input_length=MAX_SENTENCE)(input_layer)
model = layers.Bidirectional(layers.LSTM(LSTM_UNITS, recurrent_dropout=LSTM_DROPOUT, return_sequences=True))(model)
model = layers.TimeDistributed(layers.Dense(DENSE_UNITS, activation="relu"))(model)
crf_layer = CRF(units=TAG_COUNT)
output_layer = crf_layer(model)
ner_model = Model(input_layer, output_layer)
loss = losses.crf_loss
acc_metric = metrics.crf_accuracy
opt = optimizers.Adam(lr=0.001)
ner_model.compile(optimizer=opt, loss=loss, metrics=[acc_metric])
ner_model.summary()Model: "model_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 104) 0
_________________________________________________________________
embedding_1 (Embedding) (None, 104, 50) 1759000
_________________________________________________________________
bidirectional_1 (Bidirection (None, 104, 100) 40400
_________________________________________________________________
time_distributed_1 (TimeDist (None, 104, 100) 10100
_________________________________________________________________
crf_1 (CRF) (None, 104, 18) 2178
=================================================================
Total params: 1,811,678
Trainable params: 1,811,678
Non-trainable params: 0
_________________________________________________________________history = ner_model.fit(X_train, y_train, batch_size=BATCH_SIZE, epochs=MAX_EPOCHS, validation_split=0.1, verbose=2)Our model has 1.8 million parameters, so it is expected that training will take awhile.
Train on 38846 samples, validate on 4317 samples
Epoch 1/5
- 117s - loss: 0.4906 - crf_accuracy: 0.8804 - val_loss: 0.1613 - val_crf_accuracy: 0.9666
Epoch 2/5
- 115s - loss: 0.1438 - crf_accuracy: 0.9673 - val_loss: 0.1042 - val_crf_accuracy: 0.9679
Epoch 3/5
- 115s - loss: 0.0746 - crf_accuracy: 0.9765 - val_loss: 0.0579 - val_crf_accuracy: 0.9825
Epoch 4/5
- 115s - loss: 0.0451 - crf_accuracy: 0.9868 - val_loss: 0.0390 - val_crf_accuracy: 0.9889
Epoch 5/5
- 115s - loss: 0.0314 - crf_accuracy: 0.9909 - val_loss: 0.0316 - val_crf_accuracy: 0.9908Evaluation and testing
We can inspect the loss and accuracy plots from the model training. They both look acceptable and it doesn't appear that the model is overfitting. The model training could definitely benefit from some hyperparameter optimisation, but this type of fine-tuning is out of scope for this post.
plot_history(history.history)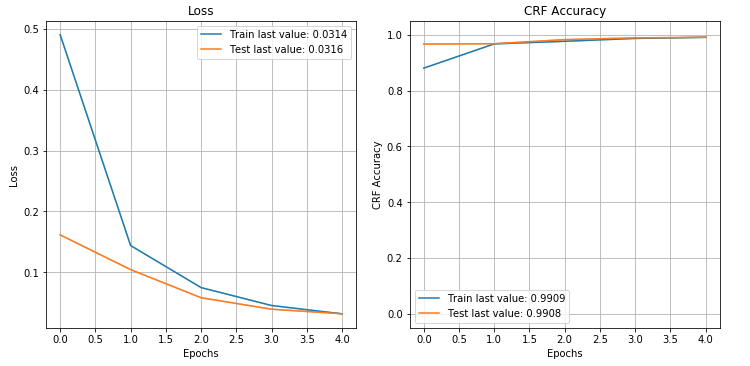
We can also test how well the model generalises by measuring the prediction accuracy on the hold-out set.
y_pred = ner_model.predict(X_test)
y_pred = np.argmax(y_pred, axis=2)
y_test = np.argmax(y_test, axis=2)
accuracy = (y_pred == y_test).mean()
print("Accuracy: {:.4f}/".format(accuracy))Accuracy: 0.9905It appears that the model is doing quite well, however this is slightly misleading. This is a highly imbalanced dataset because of the very high number of O-tags that are present in the training and test data. There is further imbalance between the samples including the various tag classes. A better inspection would be to construct confusion matrices for each tag and judge the model performance based on those. We can construct a simple Python function to assist with inspection of the confusion matrices for individual tags. We use two randomly selected tags to give us a sense of what the confusion matrices for individual tags would look like.
def tag_conf_matrix(cm, tagid):
tag_name = index2tag[tagid]
print("Tag name: {}".format(tag_name))
print(cm[tagid])
tn, fp, fn, tp = cm[tagid].ravel()
tag_acc = (tp + tn) / (tn + fp + fn + tp)
print("Tag accuracy: {:.3f} \n".format(tag_acc))
matrix = multilabel_confusion_matrix(y_test.flatten(), y_pred.flatten())
tag_conf_matrix(matrix, 8)
tag_conf_matrix(matrix, 14)Tag name: B-per
[[496974 185]
[ 441 1184]]
Tag accuracy: 0.999Tag name: I-art[[498750 0][ 34 0]]Tag accuracy: 1.000Finally, we run a manual test by constructing a sample sentence and getting predictions for the detected entities. We tokenize, pad, and convert all words to indices. Then we call the model and print the predicted tags. The sentence we use for our test is "President Obama became the first sitting American president to visit Hiroshima".
sentence = "President Obama became the first sitting American president to visit Hiroshima"re_tok = re.compile(f"([{string.punctuation}“”¨«»®´·º½¾¿¡§£₤‘’])")
sentence = re_tok.sub(r" ", sentence).split()
padded_sentence = sentence + [word2index["--PADDING--"]] * (MAX_SENTENCE - len(sentence))
padded_sentence = [word2index.get(w, 0) for w in padded_sentence]
pred = ner_model.predict(np.array([padded_sentence]))
pred = np.argmax(pred, axis=-1)
retval = ""
for w, p in zip(sentence, pred[0]):
retval = retval + "{:15}: {:5}".format(w, index2tag[p])" + "\n"
print(retval)President : B-per
Obama : I-per
became : O
the : O
first : O
sitting : O
American : B-gpe
president : O
to : O
visit : O
Hiroshima : B-geoSummary
In this blog post we covered use -cases and challenges around Named Entity Recognition, and we presented a possible solution using a BiLSTM-CRF model. The fitted model performs fairly well and is able to predict unseen data with relatively high accuracy.
References
Ramshaw and Marcus, Text Chunking using Transformation-Based Learning, 1995, arXiv:cmp-lg/9505040.
Guillaume Lample, Miguel Ballesteros, Sandeep Subramanian, Kazuya Kawakami, Chris Dyer, Neural Architectures for Named Entity Recognition, 2016, Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pp. 260-270, https://www.aclweb.org/anthology/N16-1030/
Diederik P. Kingma and Jimmy Ba, Adam: A Method for Stochastic Optimization, 3rd International Conference for Learning Representations, San Diego, 2015, https://arxiv.org/abs/1412.6980
Nikolay Manchev is the Principal Data Scientist for EMEA at Domino Data Lab. In this role, Nikolay helps clients from a wide range of industries tackle challenging machine learning use-cases and successfully integrate predictive analytics in their domain specific workflows. He holds an MSc in Software Technologies, an MSc in Data Science, and is currently undertaking postgraduate research at King's College London. His area of expertise is Machine Learning and Data Science, and his research interests are in neural networks and computational neurobiology.
Subscribe to the Domino Newsletter
Receive data science tips and tutorials from leading Data Science leaders, right to your inbox.
By submitting this form you agree to receive communications from Domino related to products and services in accordance with Domino's privacy policy and may opt-out at anytime.



