Semi-uniform strategies for solving K-armed bandits
Nikolay Manchev2022-01-31 | 6 min read

In a previous blog post we introduced the K-armed bandit problem - a simple example of allocation of a limited set of resources over time and under uncertainty. We saw how a stochastic bandit behaves and demonstrated that pulling arms at random yields rewards close to the expectation of the reward distribution.
In this article, we develop the concept further and introduce smarter strategies that potentially lead to better rewards.
Epsilon-first strategy
Epsilon-first is a two-phase strategy, where the agent starts with a purely exploratory phase, followed by an exploitation phase. The exploration phase takes place during the first \(\epsilon T\) trials, and its purpose is to get sufficient knowledge to identify the arm that provides the highest expected rewards. Once this best arm has been identified, the algorithm plays it for the remaining number of turns \((1-\epsilon)T\). During the exploration phase, the actions are either uniformly selected from \(\mathcal{A}\) or taken in order, repeatedly looping over \(\mathcal{A}\) until the end of the phase. In the latter case, we usually perform \(NK\) (\(N \in \mathbb{N}\)) iterations for the exploration phase, which guarantees equal representation of all reward distributions. This approach is given in Algorithm 1.

Algorithm 1 - Epsilon-first bandit
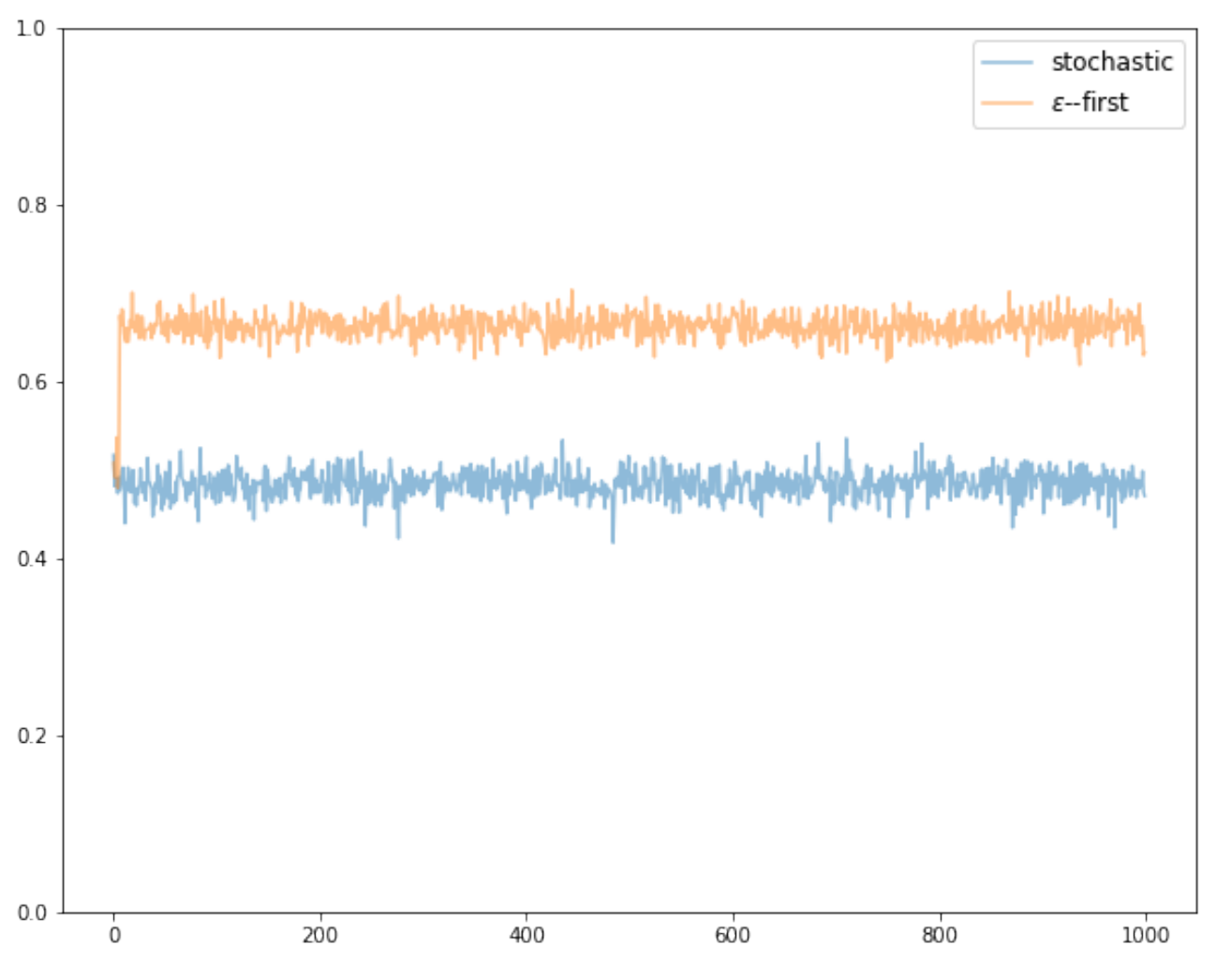
We see that the algorithm initially runs an exploration phase for \(NK\) iterations, storing the rewards at each time-step. At the end of the exploration, it sums the stored rewards over all possible arms and selects the arm that has accumulated the highest reward so far. The algorithm then switches to an exploitation phase and plays the best arm for all of the remaining time steps. Looking at the results of a simulation (Figure 1) it immediately becomes apparent that the epsilon-first strategy significantly outperforms the stochastic bandit when tested against identical reward distributions. We see that the two algorithms initially perform similarly, which is due to the uniform selection of the arms in the exploration phase of the epsilon-first algorithm. Once epsilon-first transitions to the exploitation phase, however, it immediately starts accumulating higher rewards, yielding a mean immediate reward of \(\bar{R} \approx 0.66\) and a cumulative reward \(G \approx 665\) - a significant improvement compared to the stochastic bandit approach.
Figure 1 - Stochastic vs. Epsilon-first bandits simulation with \(K=3\), \(T=1000\), and \(N=2\). Averaged over 10 games and 100 runs per game.
We need to recognize that, although Epsilon-first performs better in comparison to random selection, there are several significant issues that represent substantial drawbacks:
- An exploration phase that is too short could lead to the selection of suboptimal greedy action.
- The selection of \(\epsilon\) is external — there is currently no prescription on how long the exploratory phase should be executed for. This issue exacerbates the previous point.
- One of the key assumptions of the Epsilon-first strategy is that the reward distributions are stationary. If this assumption is violated then the agent has a very high probability of locking onto the wrong arm until time has run out.
Epsilon-greedy strategy
The epsilon-greedy is one possible improvement over the epsilon-first strategy. The key difference in this approach is that, instead of having clear-cut exploration and exploitation phases, exploration is more uniformly spread over \(T\). This is achieved by performing a random action at each time-step \(t \in T\) such that exploration is performed for \(\epsilon\) proportion of all trials and the best arm is exploited in \((1-\epsilon)\) proportion of the trials. The value of \(\epsilon\) is typically chosen as 0.1.

Algorithm 2 - Epsilon-greedy bandit
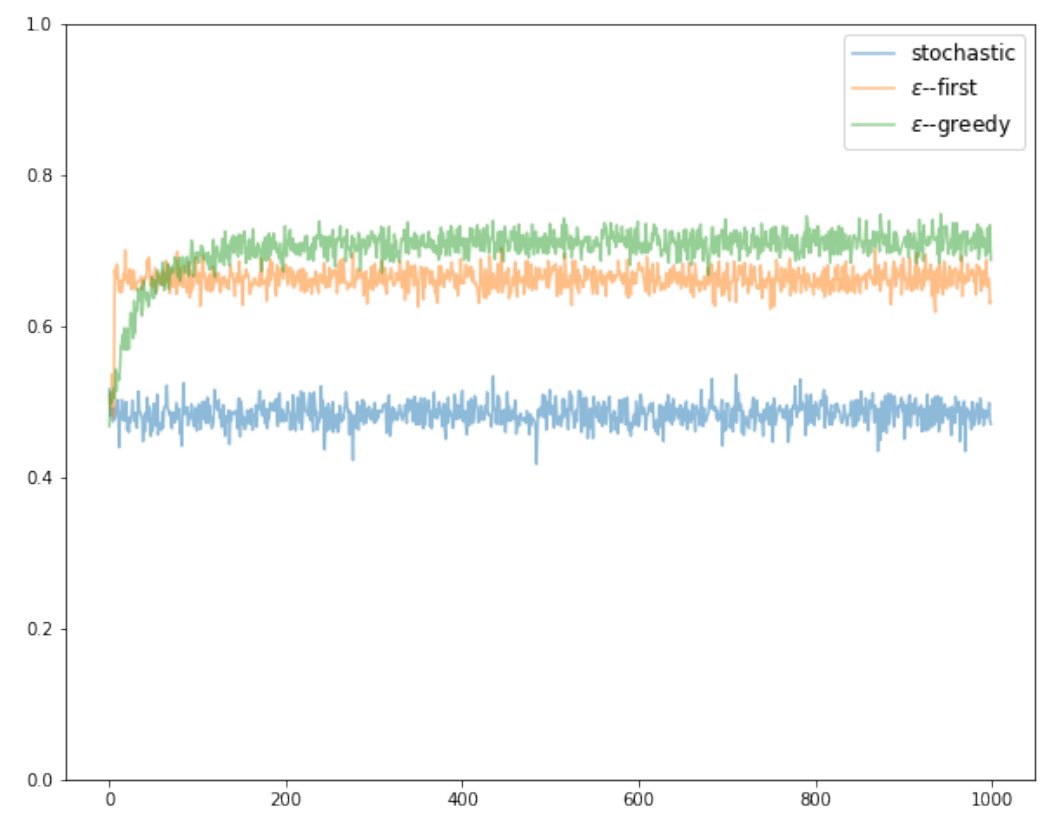
During the exploration phase an arm is randomly selected with uniform probability, and during the exploitation phase the strategy plays the arm with the highest estimated expected reward. Algorithm 2 outlines the implementation of the epsilon-greedy strategy, and Figure 2 adds epsilon-greedy's performance to the results of the simulation. We clearly see that the rewards of epsilon-greedy are initially in the range of the stochastic strategy, but as the algorithm performs a number of exploratory rounds its estimation of the expected rewards improves, and the rewards start to outperform both the stochastic and the epsilon-first strategies.
Figure 2 - Stochastic vs. Epsilon-first vs. Epsilon-greedy bandits simulation with \(K=3\), \(T=1000\), and \(N=2\). Averaged over 10 games and 100 runs per game.
Summary
In this article, we looked at two semi-uniform strategies for K-armed bandits - epsilon-first and epsilon-greedy. We showed that they both perform better than a completely random strategy that we covered in the previous post. One problem with the semi-uniform approach, however, is that these strategies do not update their exploration regime in line with the observed rewards. Intuitively, an algorithm that can adapt its decisions on the basis of the rewards so far should perform better. A simple adaptation example could be an algorithm that can dynamically decide that an arm is so underperforming that is no longer viable to be explored at all. This, and other adaptive approaches will be the topic of a future article.
Nikolay Manchev is the Principal Data Scientist for EMEA at Domino Data Lab. In this role, Nikolay helps clients from a wide range of industries tackle challenging machine learning use-cases and successfully integrate predictive analytics in their domain specific workflows. He holds an MSc in Software Technologies, an MSc in Data Science, and is currently undertaking postgraduate research at King's College London. His area of expertise is Machine Learning and Data Science, and his research interests are in neural networks and computational neurobiology.
RELATED TAGS
Subscribe to the Domino Newsletter
Receive data science tips and tutorials from leading Data Science leaders, right to your inbox.
By submitting this form you agree to receive communications from Domino related to products and services in accordance with Domino's privacy policy and may opt-out at anytime.



